„MATHESIS” A XVIII. SZÁZADI VAS MEGYÉBEN

A matematika fejlődéstörténetében a XVIII. század előtti időszak nagymértékben meghatározó. Míg az első matematikai eredményeket több ezer évvel ezelőtt a gyakorlat hívta életre (földmérés, építkezések, aztán később pénzügyi számítások, szerencsejátékok stb.), később egyre meghatározóbbá vált az axiomatikus, precíz, tudományos igényű, az absztrakcióval dolgozó felépítés. Gondoljunk csak az ókori görög geometriai eredményekre, a kora középkori arab egyenletmegoldási módszerekre, a XV. századi algebrai problémákra, a reneszánsz festészet geometriai vonatkozásaira. A XVII. századtól ismét szerepet kapott a gyakorlat – elsősorban a társtudományok, például a fizika szempontjából.¹ Newton mechanikai eredményeihez, a mozgás alapvető törvényeihez szükség volt a differenciál- és integrálszámításra. (Persze mindehhez kellettek az ókori alapok: Ptolemaiosz, Apollóniosz és Arkhimédész eredményeit Kopernikusz, Kepler és Newton is felhasználta matematikai, fizikai és csillagászati kutatásainál.)² A XVIII. század elején úgy tűnt, hogy a következő évtizedeket az előbb említett két matematikai diszciplína (a differenciál- és integrálszámítás) vizsgálatával, elmélyítésével, fejlesztésével töltik a tudósok. Ám a matematikán kívüli világból érkező igények ezt felülírták, újabb eredményeket követeltek.³ Így tudtak a gyorsan fejlődő matematikai részterületek (differenciálegyenletek, valószínűség-számítás) – a fizikán túl – a műszaki tudományokra és a technikai, ipari fejlődésre hatni.

A magyarországi matematika fejlődése a XVIII. század előtt elmaradt az európaitól. Ez elsősorban történelmi helyzetünk miatt volt így. Az 1700-as évektől kezdve viszont egyre népszerűbb tudomány lett, sokszor divat volt – nem matematikusok körében is – matematikával foglalkozni. Ismertek – többek között – a Kőszegen született bölcseleti és teológiai doktor: Rájnis József (1741–1812), a magyar történeti nyelvészet magalapítója: Révai Miklós (1730–1807), a nyelvész Sajnovics János (1733–1785) és a költő Csokonai Vitéz Mihály (1773–1805) matematikai próbálkozásai, amelyek több esetben pontatlanságokat is tartalmaztak.⁴

A matematika népszerűbbé válásához hozzájárult a magyar oktatás átalakulása. A török kiűzése után, a XVII–XVIII. század fordulójára ismét a magyar királyság határai közé kerültek vissza a korábbi hódoltsági területek, bár Erdély továbbra is önálló maradt. A katolikus és a protestáns népiskolák hálózata a XVIII. század elejére alakult ki, amelyekben az adott település nyelvén tanítottak, míg a közép- és felsőoktatásban a latin nyelvet használták. A középszintű iskolák tovább differenciálódtak: a kisgimnáziumokban latin grammatikát és matematikát oktattak, a nagygimnáziumokban mindezek (a grammatika és a matematika) mellett szerepet kapott a poétika, a retorika és a klasszikus művek tanulmányozása. A XVIII. században számos tanügyi reformra került sor. Az akadémiai bölcselet tagozaton Arisztotelész írásai helyett modernebb szerzők műveinek megismerése során találkoztak a diákok fizikával és – Apáczai Csere János javaslatára – Descartes munkásságával. Mindezek mellett helyet kapott a jezsuita és a piarista akadémiák, a protestáns kollégiumok, líceumok stúdiumaiban Galilei, Newton, Bacon, Leibnitz kutatásainak megismerése, és ennek köszönhetően erősödött a kísérleti fizika oktatása. (Gyarapodtak a fizikai szertárak, csillagvizsgálók épültek.) A jezsuita gimnáziumok tantervét is modernizálták: a történelem kísérő tárgya a földrajz lett. Nagyszombatban tankönyv is készült ehhez a két tárgyhoz. A piarista és a protestáns iskolák is ezt az irányt követték.

Az 1700-as évek második felében a népiskolák mellett más középszintű iskolák is megjelentek. Jezsuita egyetem működött Nagyszombatban és Kolozsváron, jezsuita akadémia Budán, Győrben, jezsuita nagygimnázium többek között Sopronban és Kőszegen. A piaristáknak Pesten, Veszprémben, Nagykanizsán is volt nagygimnáziumuk, a pápai nagygimnáziumot pedig pálos szerzetesek működtették. A premontreiek Csornán, a Domonkos-rendiek Vasváron alapítottak kisgimnáziumot. A protestánsok iskolahálózata is gazdag volt, az evangélikusoknak többek között Sopronban volt nagygimnáziumuk.⁵ Az oktatás további átalakítása a XVIII. század második felében történt meg – Mária Terézia és II. József intézkedéseinek köszönhetően.

A tanítás mind a gimnáziumokban, mind a bölcseleti tagozatokon latin nyelven folyt, de a XVIII. század közepétől kezdve a piarista reformerek azt javasolták, hogy középszinten magyar nyelven történjen az oktatás. Ez a törekvés a katolikusok és a protestánsok körében is népszerű volt: az anyanyelven való tanulás elérhetőbbé tette az ismeretek megszerzését, és erősítette a nemzettudatot. Mindezen törekvéseknek köszönhető, hogy – a latin mellett – magyar nyelvű tankönyvek is készültek.⁶ A protestáns iskolák tanárai magyar nyelven írtak szélesebb körnek szóló, egyszerűbb aritmetikai összefüggéseket, számításokat tartalmazó tankönyveket. Latin és német nyelven pedig a jezsuita iskolák oktatói készítettek magasabb szintű ismereteket is tartalmazó könyveket.⁷ Ebben élen jártak a nagyszombati egyetem oktatói.

A Pázmány Péter (1570–1637) által alapított egyetemen kezdettől fogva fontos szerepet kapott a matematika – elsősorban a filozófiai kurzusokban. Az egyetem oktatói számos matematikai tankönyvet írtak. Megemlítendő Berzeviczy Henrik (1652–1713) több könyve, Dubovszky János (1654–1710) és – a Kőszegen is tanító – Székely Ferenc (1658–1715) trigonometriai táblázatokat tartalmazó könyve, Jánosi Miklós (1701–1741) a síkbeli és a gömbi trigonometriát, valamint csillagászati kérdéseket tárgyaló munkája, Lipsicz Mihály (1703–1765) Algebrája, Hell Miksa (1720–1792) Aritmetikája és algebrája, valamint a Kőszegen is tanító Hertl Ignác (1702–1775) és a Kőszegen született Horváth (Keresztély) János (1732–1799) tankönyvei.⁸ A következő oldalakon az utóbbi két matematikus munkásságával foglalkozunk.

 

Hertl Ignác Szakolcán született 1702-ben, Leobenben, Bécsben és Nagyszombatban tanult. Húszévesen kötelezte el magát a jezsuita értékek mellett, ezek szellemiségében oktatott. Tanári hivatása mellett volt házigondnok, könyvtáros, tábori lelkész, valamint a váci püspök gyóntatója és tanácsadója. Sopronban, Nagyszombatban, Budán, Kassán és Kőszegen tanított matematikát – több helyen fizikát, dialektikát, metafizikát. Kőszegre 1761-ben került. Itt is volt házigondnok, könyvtáros, valamint házi lelkiatya és magyar–német lelkipásztor. Az 1775-ben bekövetkezett haláláig Kőszegen élt.⁹

Hertl Ignác aritmetikával és algebrával foglalkozó latin nyelvű könyve, az Elementa arithmeticae numericae et literalis practicae et theoricae in usum discentium proposita 1753-ban jelent meg Kassán Vajkovics Imre (1715–1796) teológus, a nagyszombati egyetem tanára, kalocsai nagyprépost közreműködésének köszönhetően.

A könyv rövid bevezetővel kezdődik. Hertl megemlíti, hogy elemi algebrával és aritmetikával sok könyv foglalkozik – némelyek túl röviden vagy túl hosszan. Ő azt tűzte ki célul, hogy a könyve az iskolákban jól alkalmazható tankönyv legyen.

A matematikai rész mindezek figyelembevételével indul. Hertl alapvető ismereteket, definíciókat rögzít, amelyek az alapműveletekre (összeadás, szorzás) és a természetes számokra vonatkoznak. Számelméleti fogalmakat is tisztáz: előkerülnek – többek között – az oszthatóság és a prímszámok kérdései, a prímtényezős felbontás és a közös osztók. Olvashatunk arról, hogy tízes számrendszerben, a ma is jól ismert hindu–arab számjegyeket használva dolgozunk. Mindez megjelenik a helyi értékes számírás során és a számok elnevezésében. Az első fejezetben példákat találunk arra, hogyan kell a különböző műveleteket írásban elvégezni. Részletesen ismerteti a 4562 + 4634 + 8532 = 17728 összeg, a 4568 – 3654 = 914 különbség, a 354 × 34 = 12036 szorzat kiszámításának módját. A szorzás megkönnyítésére szolgáló szorzótáblázatot is megtaláljuk a könyvben.¹⁰

Hertl az osztásra külön hoz példát a maradék nélküli és a maradékos esetben: a korábbi szorzásra hivatkozva megadja a 12036 : 34 = 354 eredményt, míg a 12049 : 34 esetben a hányados 354, a maradék 13 lett. Így ha a 12036-ot elosztjuk 34-gyel, akkor a 354-es egész részhez tartozik még 13/34 törtrész is.¹¹

A következőkben a műveletekről olvashatunk. Hertl megadja az egyes műveletek jelét: az összeadásét (A + B), a kivonásét (A – B), a szorzásét (A × B), az osztáséval együtt pedig a törtek jelölését is (a/b). Értelmezi a számok közötti relációkat (A = B, A > B, A < B), és a végtelen fogalmával is találkozhatunk. Az a triviálisnak tekinthető állítás is olvasható, hogy ha bármelyik számból kivonjuk saját magát, akkor az eredmény a 0 lesz, és a különböző előjelű számok szorzásaként kapott eredmény előjeléről is olvashatunk, majd az algebrai kifejezések közötti műveletek elvégzésére láthatunk példákat. Az a + 2b – 3c + d kifejezéshez hozzáadja a 2a – 2b + 3c – d kifejezést, és az eredmény 3a + d lesz (az egyneműek összevonhatóságának köszönhetően). Az algebrai kifejezések kivonására is mutat példát. Az a + 3b – 4c kifejezésből kell kivonnunk a d + 3b + 3c kifejezést. Ehhez a szerző először a második kifejezés ellentettjét veszi, és ezt adja hozzá az első kifejezéshez, így az eredmény a – d – 7c lesz. Az algebrai kifejezések szorzására is láthatunk néhány példát – először a nevezetes azonosságok segítségével. Az a + b kifejezést saját magával szorozza Hertl, azaz az (a + b)(a + b) szorzat eredményét keresi. Ehhez az első tényező első tagjával végigszorozza a második tényező tagjait (így írja: aa + ab, ahol az aa az a²-et jelenti), majd az első tényező második tagjával szorozza meg a második tényező tagjait (ab + bb). Végül ezt a két eredményt – az ismert módon – összeadja, így aa + 2ab + bb (azaz a² + 2ab + b²) lesz a megoldás.¹² Láthatunk példákat algebrai kifejezések osztására, algebrai törtek egyszerűsítésére. Hertl az a + 2ab kifejezést osztja a-val (az eredmény 1 + 2b), majd az aa – bb (azaz az a² – b²) kifejezést osztja el az a + b kifejezéssel (az eredmény a – b).¹³

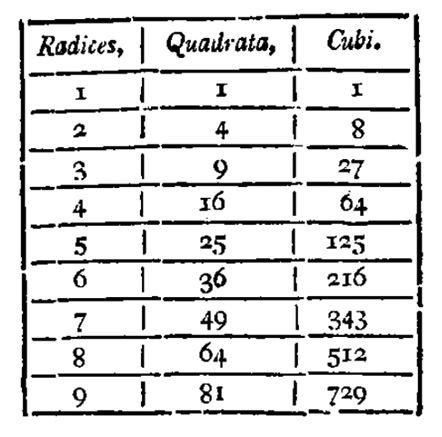
Olvashatunk a pozitív egész kitevőjű hatványozásról, a gyökvonásról, annak elvégezhetőségéről és geometriai alkalmazhatóságáról is. Hertl külön táblázatban adja meg az 1-től 9-ig tartó egész számok második, harmadik és negyedik hatványának értékét.¹⁴

Ügyes algoritmikus számítással azt is megmutatja, hogyan határozható meg például a 49 801 249 négyzetgyöke (7057).¹⁵ Majd a 14 négyzetgyökét (amely irracionális szám) is meghatározza három tizedes jegy pontossággal (3,741).¹⁶ Ezek után a harmadik hatványra vonatkozó ismeretek, ötletek jönnek. Találkozhatunk az (a + b)³ = a³ + 3a²b + 3ab² + b³ nevezetes azonossággal, és a 12 812 904 köbgyökének (amely a 234) meghatározási módjával.¹⁷

A következő fejezet az elsőfokú egyenletekről, egyenletrendszerekről szól. Először az egyenletmegoldás során használt mérlegelv szabályait tisztázza Hertl, majd kitér az ismeretlenek jelölési módjára is (az x, y és z a leggyakrabban használtak).¹⁸ Megoldja az x + 2x + 3x + 3 = 63 egyenletet (x = 10)¹⁹, majd az x + y = 6 és 2x = y egyenletekből álló egyenletrendszert (x = 2 és y = 4)²⁰.

A tankönyv második része a törtekről szól, amelyeket arányok segítségével vezet be a szerző. Több példát is ad az arányok, hányadosok megadására – mindezeket vegyes törtalakban is felírja (például ha a 17 : 5 hányadosra vagyunk kíváncsiak, akkor a 3 egészhez még 2/5 kell)²¹. Megjelenik a törtek egyenlősége, a törtek egyszerűsítése, bővítése, és ezek kapcsán Hertl egyszerűbb egyenleteket is megold (például a 2/x = x/8 esetben az x = 4 eredmény születik)²², több esetben általános felírást, képletet is közöl (például az a/x = c/b összefüggésből az x = (ab)/c következik)²³. Ezekhez gyakran szöveges problémákat is társít.

Hertl Ignác matematikakönyvének harmadik része is a törtekről szól, itt már összetettebb kérdések is előkerülnek. Olvashatunk a közös nevező megtalálásáról, amelyhez a törteket megfelelő módon kell bővíteni (például az 1/2, a 2/3 és a 3/5 esetében 30 lesz a közös nevező, emiatt az 1/2 esetében 15-tel szorozzuk a számlálót és a nevezőt, a 2/3 esetében 10-zel, a 3/5 esetében 6-tal, és így kapjuk meg a bővített törteket: 15/30, 20/30 és 18/30, amely átírások a törtek nagyságrendi összehasonlítását is lehetővé teszik)²⁴. A törtek összeadásának módja is ebben a részben kerül elő. Ehhez közös nevezőre van szükség, amelynek megadási módját Hertl korábban ismertette. A példájában a 2/3 és a 3/4 összegzése szerepel. A megfelelő bővítés után a 8/12 és a 9/12 összeadása szükséges, amely 17/12-et eredményez. Mindezek leírása általánosan is szerepel. Az a/b és c/d alakú törtek összege: (ad + bc)/(bd).²⁵ Ezek után a törtek különbségének megadása sem túl nehéz – Hertl ezt is bemutatja éppúgy, mint a törtek szorzásának a módját. A törtek osztását a következőképpen magyarázza. Ha az a/b törtet el kell osztanunk a c/d törttel, akkor bővítsük az első törtet (ad)/(bd), a másodikat (bc)/(bd) alakúra. Ezek után a számlálókat osztjuk egymással, ebből (ad)/(bc) lesz, majd a nevezőket osztjuk egymással, amely 1-et eredményez. Ekkor az eredeti két tört hányadosa (ad)/(bc).²⁶ Olvashatunk a vegyes törtalakban megadott törtek összeadási módjáról is – külön az egészrészek és külön a törtrészek összegét vette Hertl. Az ilyen típusú törtek szorzása is szerepel a könyvben.

A következő fejezet a tizedes törtek elméletét tartalmazza. Hertl ír a helyi értékekről (a tizedekről, századokról, ezredekről stb.), és szerepet kap a tizedes törtekkel kapcsolatos műveletek elvégzésének bemutatása.²⁷ A következő fejezetben találkozhatunk olyan elsőfokú egyenletekkel, (két- és háromváltozós) egyenletrendszerekkel, amelyek már törteket is tartalmaznak (akár együtthatóként, akár eredményként). Természetesen most is gyakran szöveges feladatok formájában találkozunk az egyenletekkel, egyenletrendszerekkel. Egy ilyen egyszerűbb feladat az alábbi. Péter háromszor annyi idős, mint Pál. Antal életkora Pál életkorának hatszorosánál három évvel több. A három ember életkorának összege 153. Hány évesek külön-külön?²⁸

A könyv utolsó részében másodfokú egyenletekkel találkozhatunk. Hertl az xx + 2x = 99 (azaz az x² + 2x = 99) egyenlet megoldásánál nem a másodfokú egyenlet megoldóképletét, hanem a kora középkori arab matematikusok által bemutatott kiegészítő eljárást alkalmazta. Észrevette, ha az egyenlet bal oldalát kiegészíti 1-gyel, akkor nevezetes azonosságot kap: x² + 2x + 1 = (x + 1)². De ekkor növelnie kell az egyenlet jobb oldalát is 1-gyel: 99 + 1 =100. Az egyenlet mindkét oldalát egyforma mértékben változtatta, így az egyenlőség a továbbiakban is fennáll, azaz (x + 1)² = 100. Innen (a négyzetgyökvonások után) azt kapta, hogy x + 1 = 10, azaz x = 9.²⁹ Bonyolultabb volt a 3x² + 2x = 3333 egyenlet megoldása. Itt is az előbbi módszert alkalmazta Hertl.³⁰ A könyv néhány hasonló egyenlet megoldásával zárul.

Hertl Ignác tankönyvében megközelítőleg 140 oldalon ismertetett – főleg a gyakorlati életben is hasznos – matematikai ismereteket. Az algebra, az aritmetika, a számolás elősegítése volt a célja, azaz valóban az iskolások számára jól használható könyvet írt.

Ezek után egy XVIII. századi, Vas megyéhez köthető másik matematikus eredményeivel ismerkedhetünk meg.

 

Horváth (Keresztély, néhol röviden csak Ker.) János Kőszegen született 1732-ben. A jezsuita rendbe 1751-ben lépett be. Nagyszombatban és Budán volt egyetemi tanár, a bölcsészeti kar dékánja, majd a budai egyetem rektora lett. Nyugdíjazása után egresi apáttá nevezték ki. A matematika mellett tanított természettant és fizikát is – több ilyen témájú tankönyvet írt. A felsőbb fizika, a kísérleti fizika és a mechanika tanára volt, az 1782-ben létrejött Mérnökképző Intézetben is tanított, itt is írt tankönyveket a hallgatók számára. Halála előtt kilenc évvel, 1790-ben a göttingeni tudós társaság levelező tagjává választotta. Immanuel Kant filozófiájának első magyar bírálója volt. Tankönyvíróként igen termékeny, több munkáját külföldön is kiadták – így Augsburgban és Velencében. A hegységek keletkezéséről, a vulkanizmusról, a légkörről, a vízrajzról és a földrengések okairól szóló fizikakönyve még Goethére is nagy hatást tett. Horváth tankönyveiben az addigi ismereteket precízen rendszerezte.³¹

Legjelentősebb matematikai témájú, latin nyelvű tankönyve az Institutiones matheseos, philosophiae auditorum usibus accommodatae, amely 1773-ban jelent meg Nagyszombatban, majd 1782-ben Augsburgban is kiadták. A (több mint 450 oldalas) tankönyv bevezetése a matematika felépítésének módját tárgyalja: a definíciók, axiómák, posztulátumok, hipotézisek, tételek, lemmák stb. szerepét elemzi a szerző. A pontos definiálás után van lehetőség – az axiómák és a feltételek felhasználásával – a tételek bizonyítására. A négyoldalas bevezetőben a matematika tanulásához is kapunk tanácsokat: a tankönyv felépítését, az ott leírtak sorrendjét érdemes szem előtt tartani.³²

A tankönyv első része az aritmetikai ismereteket tartalmazza. Megtaláljuk az arab-hindu és a római számírás módjának leírását, a helyi értékek értelmezését, azok elnevezését. Külön fejezet szól az összeadásról, kivonásról, szorzásról és osztásról, azok tulajdonságairól. A műveletek írásbeli elvégzésére sok példát mutat a szerző. Horváth tankönyvében is találunk szorzótáblát.³³

Az osztás értelmezése során – a nem maradék nélküli eset kapcsán – a törtek is előkerülnek. Az aritmetikai rész utolsó fejezetében a mértékegységek és az átváltások szerepelnek (többek között a hosszúság, tömeg és az idő mérésére vonatkozóan).³⁴ Mérési feladatokat is bemutat a szerző.

A tankönyv második nagyobb egysége az algebrai ismereteké. Az első fejezetben megtörténik a – számokat helyettesítő – változók (betűk) és a matematikai szimbólumok (például: +; −;×; =; ∞) bevezetése. Találkozunk feladatokkal algebrai kifejezések összevonására és kivonására; például a 3a²b + 2cd – fg, a 2a²b – 3cd + fg és az ab² – cd + df kifejezések összege az 5a²b + ab² – 2cd + df kifejezés lesz.³⁵ Az algebrai kifejezések szorzásának bevezető példája az a + 2b – c és az a – 2b szorzat megadása. Horváth azt javasolja, hogy először a második tényező első tagjával (a) szorozzuk végig az első tényező mindegyik tagját (a² + 2ab – ac lesz az eredmény), majd a második tényező második tagjával (– 2b) szorzunk (– 2ab – 4b² + 2bc az eredmény), és a végeredmény megadásához a kapott két kifejezést adjuk össze. Azaz a szorzat: a² – ac – 4b² + 2bc.³⁶ Külön fejezet szól az algebrai törtek osztásáról, egyszerűsítéséről – szintén több (köztük néhány komolyabb) példával illusztrálva.

Olvashatunk a természetes és a tört számok közötti relációkról, azok összehasonításáról. A törtek esetében közös nevezőt kell találnunk. Az 1/3 és a 2/5 összehasonlításánál a 15 lesz a közös nevező, ehhez az első törtet 5-tel, a másodikat 3-mal bővítjük, így már az 5/15 és a 6/15 közötti reláció megadása a feladat. (Természetesen a 6/15, azaz a 2/5 a nagyobb.)³⁷ A fejezetben a törtek bővítésének általános megadása, a törtek közötti műveletek eredményének kiszámítása is helyet kap.

A tankönyv algebrai részének második fejezetében találkozunk a hatványozás, a gyökvonás fogalmával és ezek azonosságaival. Horváth megadja a nulla, a negatív egész és a törtkitevőjű hatvány fogalmát – mindegyiket példákkal szemléltetve és az általános formulát ismertetve. A nevezetes azonosságok is ebben a fejezetben szerepelnek, a szorzattá alakításnál és a törtek egyszerűsítésénél jelennek meg: például a 4a⁴ + 12a²b + 9b² osztható 2a² + 3b-vel, mert (2a² + 3b)² = 4a⁴ + 12a²b + 9b².³⁸ A számítások megkönnyítése érdekében külön táblázat található a könyvben, amely a második és harmadik hatványok értékét adja meg.³⁹

A táblázat segít a pozitív egész hatványkitevő megtalálásánál is, ha ismerjük az alapot és az értéket. Több példán keresztül mutatja meg ezt az algoritmust Horváth. Így – többek között – végiggondolhatjuk, hogy a 23-nak miért a harmadik hatványa a 12 167.⁴⁰ Mindezek mellett a törtkitevőjű hatványok megadása és használata is igen alapos, részletes.

A következő algebrai fejezet az egyenletekről, azok rendezéséről, a mérlegelvről, az ekvivalens átalakításokról szól. Itt találjuk meg az x + x/2 + (x – d)/4 = a paraméteres egyenlet gyökének megadását, az x = (4 + d)/7 eredmény levezetését. A helyettesítési értékek használata is szerepet kap. Ha az előbbi egyenletben az a helyére 80, a d helyére 30 kerül, akkor az x értéke 50 lesz.⁴¹

Egyenletrendszerek megoldásával is találkozhatunk. Horváth részletesen levezeti – többek között – az x + y = a, az y + z = b és az x + z = c háromismeretlenes egyenletrendszer gyökeinek megadását.⁴² Gyakorlati jellegű, szöveges feladatok megoldása során is használja a szerző az egyenletrendszereket. (Például: melyik lehet az a két pozitív egész szám, amelyek szorzatához hozzáadva az összegüket 79-et kapunk, azaz mi lehet az xy + x + y = 79 egyenlet megoldása a pozitív egész számok halmazán.)⁴³

A másodfokú egyenletek gyökeinek meghatározása is része a tankönyvnek. Az általános megoldóképlettel ebben a könyvben sem találkozunk, hanem különböző alakú, típusú másodfokú egyenletek megoldási módját láthatjuk. Így például szerepel az x² + 2ax = b és az x² – 4ax + 4a² = 2b paraméteres egyenlet gyökeinek maghatározása. Kétváltozós egyenletek megoldására is láthatunk példát a pozitív egész számok körében: Horváth megadja az x² + xy = a egyenlet általános megoldását (x értékét az y függvényében, ahol az a paraméter).⁴⁴

Több fejezeten keresztül olvashatunk az arányokról. Konkrét számpéldák és ismeretlent tartalmazó egyenletek is előfordulnak, így a – Hertl Ignác könyvében is megtalálható – 2 : x = x : 8 egyenlet (pozitív egész) gyökének megadása.⁴⁵ Az arányok a hatványozás és a gyökvonás azonosságaival kapcsolatosan is szerepet kapnak, és gyakorlati, szöveges problémák is megjelennek, amelyeket Horváth legtöbbször egyenletek segítségével old meg.

Ezek után a számtani és mértani sorozatok elmélete következik. A számtani sorozatok elemeit a, a + d, a + 2d, a + 3d, a + 4d stb. alakban adja meg a szerző. A mértani sorozatok elemeinek megadása pedig a, am, am², am³, am⁴ formában történik.⁴⁶ A határérték fogalma is előkerül, az 1/∞ értékét Horváth 0-nak adja meg, így lehetősége nyílik végtelen sorok összegének számítására: az 1 + 1/2 + 1/4 + 1/8 + 1/16 +...+ 1/∞ összeg értékét kiszámolva 2-t kap.⁴⁷ (Ehhez előzetesen megadja a szükséges – 1-nél kisebb, pozitív kvóciensű végtelen mértani sorokra vonatkozó – képletet.)

A tankönyv a tizedes törtek elméletével, az azok közötti műveletekkel folytatódik – természetesen itt is rengeteg példával. Találkozunk véges és végtelen tizedes törtekkel, ezek felírási módjával.

Az algebrai rész utolsó fejezete a logaritmusról szól, amelynek definiálásához a 10 hatványait használja a szerző. Az értelmezés mellett jó néhány számpélda található, amelyekhez Horváthnak logaritmustáblázatokra van szüksége: így például olvashatjuk, hogy a 10-nek kb. 0,3010300-adik hatványa lesz 2.⁴⁸ Ezzel a témával zárul a több mint 200 oldalas aritmetikai-algebrai rész a tankönyvben.

A tankönyv következő nagyobb egysége tehát a geometriáé – erre is több mint 200 oldal jut. A bevezetésben a geometria axiómarendszerének alapfogalmai és állításai szerepelnek kellő részletességgel és alapossággal. Olvashatunk pontokról, egyenesekről, a szögek méréséről, a szögek közötti kapcsolatokról, a párhuzamos egyenesek elméletéről. Ehhez köthető tételek és bizonyítások is megtalálhatók a könyvben, bár ezek mellett ábrákat nem találunk, csak a tankönyv végén van egy ábragyűjtemény. (Egy-egy ábrára több tételnél, feladatnál is hivatkozik Horváth.) Külön fejezet foglalkozik a körrel és részeivel, a kör és egyenesek kapcsolatával.

A háromszögekkel kapcsolatos rész a belső szögek összegének megadásával indul. (A 180°-os szögösszeget a párhuzamosság fogalma nélkül, a korábban belátott körökkel kapcsolatos tételekkel bizonyítja Horváth.) Ezek után találkozunk az oldalak, az oldalak és szögek kapcsolatáról szóló tételekkel, majd egybevágó és hasonló háromszögekről esik szó. A fejezet végén a háromszögek területének megadási módja is olvasható. (A legismertebbet találjuk ott: a háromszög területét egy oldallal és a hozzá tartozó magassággal számolja a szerző.)

A háromszögek mellett a négyszögekkel kapcsolatos ismeretek kidolgozása is alapos, és külön fejezet foglalkozik a szabályos sokszögekkel. Horváth megemlíti, hogy a szabályos sokszögek – a köré és beírható kör középpontjából – egybevágó, egyenlő szárú háromszögekre bonthatók, amelyek szárszöge könnyen kiszámítható. Példaként említi, hogy a szabályos ötszög középponti háromszögeinek szárszöge 360°/5, azaz 72°-os.⁴⁹

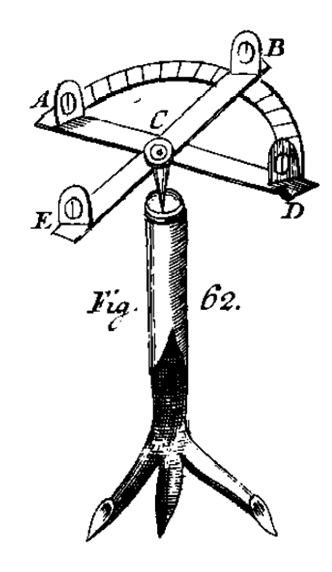
Az elemi síkgeometria után a trigonometriai ismeretek bemutatása következik, amelyek során szerepet kap a mérések fontosságának hangsúlyozása. Erre hivatkozva bizonyítja Horváth a sinustételt.⁵⁰ A fejezetnek része a szögfüggvényértékek megadási módjának ismertetése és a visszakeresés módszerének bemutatása. Itt is – mint a tankönyvben olyan sokszor – példákkal és az olvasó számára kitűzött (gyakran mérési, gyakorlati jellegű) feladatokkal dolgozik a szerző, amelyek kapcsán mérőeszközöket is bemutat. Ilyen a könyvben goniometrico néven említett szögmérő műszer⁵¹, amelynek képét megtaláljuk a függelékben.⁵²

A síkgeometriai fejezet harmadik részében területszámítási problémákkal, feladatokkal találkozunk. Ehhez Horváth levezeti a nevezetes négyszögek (így a paralelogramma és a trapéz) területének kiszámítási módját. A kör területének megadásánál a π értékét a 355 : 113 aránnyal közelíti (ez hat tizedes jegy pontossággal helyes), amely Adrianus Metius (1571–1635) holland matematikustól származik.⁵³

A jól ismert Pitagorasz-tétel (amely szerint a derékszögű háromszögekben a két befogó négyzetének összege az átfogó négyzetével egyenlő) a tankönyv 62. tétele.⁵⁴ A bizonyítás nem a mai középiskolai tankönyvekben legtöbbször előforduló, egybevágó négyzetek különböző felosztásával dolgozó változat, hanem Horváth valójában a befogótételt hívja segítségül. A példájában azt az egyenlő szárú, derékszögű háromszöget használja, amelynek befogói 2 egység hosszúak. (Érdekes, hogy a tétel megadása során Pitagorasz nevével nem találkozunk.)

Az elemi geometriai rész utolsó két fejezete a térgeometriához köthető. Találkozunk itt a jól ismert, nevezetes testek (például a kocka, a gúla, a henger), a szabályos testek bemutatásával, azok felszínének és térfogatának megadási módjával. Ezek kapcsán Horváth több korábbi algebrai ismeretre is hivatkozik (például a gyökvonásra, a nevezetes azonosságokra).

Horváth János tankönyvének utolsó nagyobb része (43 oldalon keresztül) a kúpszeletekről szól. Természetesen először az ellipszis, a parabola és a hiperbola értelmezése történik meg – azok meghatározó adataival, tulajdonságaival, a pontjaik szerkesztési módjával együtt. Több képlettel találkozunk, amelyek a kúpszeleteknek a koordináta-geometriában használt egyenleteire emlékeztetik az olvasót (például a parabola esetében az y² = px összefüggéssel⁵⁵). Mindezek mellett az érintők is szerepet kapnak, amelyek a függelék több ábráján is jól láthatók.⁵⁶

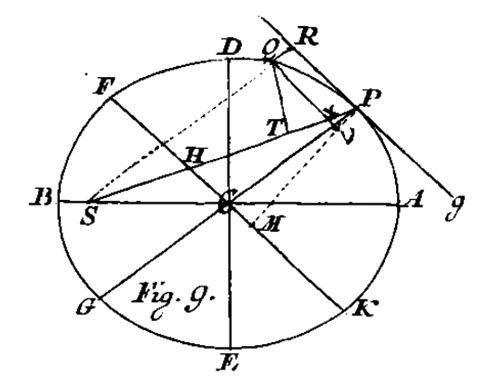
A kúpszeletekkel kapcsolatos tudnivalókkal a tankönyv véget ér. A jól szerkesztett, tömör és alapos munka gyakorlatilag a mai középiskolás matematikai tananyagot tartalmazza, esetenként túlmutat a középszintű ismereteken. A tízoldalas függelék ábrái segítik a geometriai ismeretek megértését.

Emlékezzünk meg Horváth (Keresztély) Jánosnak egy másik latin nyelvű matematikai témájú írásáról is. A Calculus orgyae civilis a nagyszombati egyetem Budára költöztetése után készült, 1780-ban adták ki Budán. A szerző 24 oldalon az akkori hossz-, terület- és térfogat-mértékrendszert tárgyalja, átváltásokkal és példákkal illusztrálva.

A hosszmértékrendszer felépítéséhez az öl („orgya”), láb („pes”), hüvelyk („digitus”), vonal („linea”) és pont („punctum”) fogalmakat használja, és ehhez jelöléseket is alkalmaz a következőképpen: 1 öl = 1º, 1 láb = 1’, 1 hüvelyk = 1’’, 1 vonal = 1’’’ és 1 pont = 1^IV. Horváth az első bekezdésben egy konkrét példával is szolgál: értelmezi, mit jelent az 5º 3’ 2’’ 4’’’ 5^IV jelölés.⁵⁷ A terület mérésére a négyszögöl, négyszögláb, négyszöghüvelyk, négyszögvonal stb. szolgál. Ilyen esetekben a jelölésnél a ◻ szimbólummal egészíti ki a hosszúság mérésénél megismert jelet, például 1 négyszögöl = 1º◻. Térfogat mérésénél a köböl, köbláb, köbhüvelyk stb. a használatos. A térfogatérték jelölésekor a ⊠ szimbólum kerül a hosszmértékeknél alkalmazottak mögé, azaz például 1 köböl = 1º⊠.

A megfelelő átváltásokkal is találkozhatunk a könyvben. Ez az alábbiakat jelenti a hosszúság mérése esetében:

1° = 6’ (1 öl 6 lábbal egyenlő);

1’ = 12’’ (1 láb 12 hüvelykkel egyenértékű);

1’’ = 12’’’ (1 hüvelyknek 12 vonal felel meg);

1’’’ = 12^IV (12 pont ad ki 1 vonást).

Természetesen a területértékek megadásához szükséges mértékegységek közötti átváltások is megjelennek.⁵⁸ A változás ebben az esetben négyzetes, azaz

1°◻ = 6 × 6 = 36’◻ (1 négyszögöl 36 négyszöglábbal egyenlő);

1’◻ = 12 × 12 = 144’’◻ (1 négyszöglábnak 144 négyszöghüvelyk felel meg);

1’’◻ = 12 × 12 = 144’’’◻ (1 négyszöghüvelyk 144 négyszögvonallal egyezik).

A térfogat mérésére megadott mértékek átváltásának levezetését is megtaláljuk Horváth könyvében.⁵⁹ Ebben az esetben köbös (harmadfokú) változás lép érvénybe:

1°⊠ = 6 × 6 × 6 = 216’⊠ (1 köbölnek 216 köbláb felel meg);

1’⊠ = 12 × 12 × 12 = 1728’’⊠ (1 köblábat 1728 köbhüvelyk ad ki);

1’’⊠ = 12 × 12 × 12 = 1728’’’⊠ (1 köbhüvelyk 1728 köbvonallal egyenlő).

Az átláthatóság kedvéért – a könyvben található további példák levezetése előtt – Horváth egy átváltási táblázatot is mellékel az alábbi formában.⁶⁰

A rövid tanulmány segítségül szolgált azoknak, akik a mérések során, a gyakorlati problémák megoldásánál, a mindennapokban szerettek volna eligazodni a mértékegységek világában. Horváth János írása a Magyarországon használt mértékegységrendszer egységesítését is elősegítette, azt egyértelműbbé tette.

A fent említett szerzők munkássága, az általuk írt tankönyvek is hozzájárultak ahhoz, hogy a XVIII. században egyre népszerűbb lett a matematika. Csokonai Vitéz Mihály egyik beszédében így méltatta ezt a tudományt: „A Mathesis, Uraim, minden Vallásba, minden Országba, minden rend és gondolkodás formájába egy. Láttál-e oly ostoba babonást, vagy oly vakmerő Eretneket, aki valamely ágazatját tagadta volna? Tudsz-é oly különböző rendtartású Országot, melyben a Mathesis igazságairól ártikulusokat (=törvénycikkeket) hoztak volna, és vagy ez, vagy más cikkelye változást vagy tilalmat szenvedett volna? Se Klima, se Temperamentum, sem Társalkodás, sem Nevelés, sem Praeiudicium nem fonhat oly látást változtató ködöt ennek mindenfelé kiderült Egén, mint a milyennel bármi a Vallásnak, a Bölcselkedésnek és a törvénykezésnek, néha vékony homállyal, néha feketés felhőkkel borongó horizonja. Ezért megérdemli ő a tiszteletet, minden bizonytalanságot, viszálkodást és tilalmazott elmélkedést kerülni óhajtó lélektől. Ezért lettem én is az ő felemelt gondolkodású híveinek, a kételkedésen kívül tétetett igazságokon, az értelem rendes nyomain, követője.”⁶¹

Csokonai szavai is megerősítik mindazt, amit a XVIII. századi, az előbbiekben megismert Vas megyei és mindenkori matematikusok képviselnek: a logikus következtetések és helyes bizonyítások, a ráció, az ész és értelem fontosságát.

   

FELHASZNÁLT IRODALOM

FILEP 2001
	FILEP László: A tudományok királynője (A matematika fejlődése). TYPOTEX Kiadó, Budapest, 2001. 2. kiadás
GINDIKIN 2003
	GINDIKIN, Simon: Történetek fizikusokról és matematikusokról. TYPOTEX Kiadó, Budapest, 2003.
HERTL 1753
	HERTL Ignác: Elementa arithmeticae numericae et literalis practicae et theoricae in usum discentium proposita. Kassa, 1753.
HORVÁTH 1780
	HORVÁTH (Keresztély) János: Calculus orgyae civilis. Buda, 1780.
HORVÁTH 1782
	HORVÁTH (Keresztély) János: Institutiones matheseos, philosophiae auditorum usibus accommodatae. Augsburg, 1782.
MÉSZÁROS–NÉMETH–PUKÁNSZKY 1999
	MÉSZÁROS István – NÉMETH András – PUKÁNSZKY Béla: Bevezetés a pedagógia és az iskoláztatás történetébe. Osiris Kiadó, Budapest, 1999.
SZÉNÁSSY 2008
	SZÉNÁSSY Barna: A magyarországi matematika története a 20. század elejéig. Polygon Kiadó, Szeged, 2008. 3. kiadás
van der WAERDEN 1977
	B. L. van der WARDEN: Egy tudomány ébredése. Gondolat Kiadó, Budapest, 1977.

   

JEGYZETEK

1	SZÉNÁSSY 2008. 70. old.
2	van der WAERDEN 1977. 16. old.
3	GINDIKIN 2003. 7. old.
4	SZÉNÁSSY 2008. 71. old.
5	MÉSZÁROS–NÉMETH–PUKÁNSZKY 1999. 329–330. old.
6	MÉSZÁROS–NÉMETH–PUKÁNSZKY 1999. 328. old.
7	FILEP 2001. 196. old.
8	SZÉNÁSSY 1998. 25–26. old.
9	SZÉNÁSSY 1998. 348. old.
10	HERTL 1753. 20. old.
11	HERTL 1753. 2–24. old.
12	HERTL 1753. 24–31. old.
13	HERTL 1753. 34. old.
14	HERTL 1753. 38. old.
15	HERTL 1753. 42–43. old.
16	HERTL 1753. 43–44. old.
17	HERTL 1753. 44–46. old.
18	HERTL 1753. 48–49. old.
19	HERTL 1753. 49–50. old.
20	HERTL 1753. 51. old.
21	HERTL 1753. 54. old.
22	HERTL 1753. 67. old.
23	HERTL 1753. 81. old.
24	HERTL 1753. 94. old.
25	HERTL 1753. 97. old.
26	HERTL 1753. 100. old.
27	HERTL 1753. 109–116. old.
28	HERTL 1753. 119. old.
29	HERTL 1753. 139. old.
30	HERTL 1753. 140–141. old.
31	SZÉNÁSSY 1998. 349. old.
32	HORVÁTH 1782. 1–4. old.
33	HORVÁTH 1782. 19. old.
34	HORVÁTH 1782. 35–36. old.
35	HORVÁTH 1782. 51. old.
36	HORVÁTH 1782. 55. old.
37	HORVÁTH 1782. 71. old.
38	HORVÁTH 1782. 96. old.
39	HORVÁTH 1782. 100. old.
40	HORVÁTH 1782. 113. old.
41	HORVÁTH 1782. 131–132. old.
42	HORVÁTH 1782. 141. old.
43	HORVÁTH 1782. 147. old.
44	HORVÁTH 1782. 158. ol
45	HORVÁTH 1782. 167. old.
46	HORVÁTH 1782. 200–202. old.
47	HORVÁTH 1782. 205. old.
48	HORVÁTH 1782. 216. old.
49	HORVÁTH 1782. 302. old.
50	HORVÁTH 1782. 315. old.
51	HORVÁTH 1782. 333. old.
52	HORVÁTH 1782. 469. old.
53	HORVÁTH 1782. 365. old.
54	HORVÁTH 1782. 367. old
55	HORVÁTH 1782. 441. old.
56	HORVÁTH 1782. 474. old.
57	HORVÁTH 1780. 3. old.
58	HORVÁTH 1780. 4. old.
59	HORVÁTH 1780. 4. old.
60	HORVÁTH 1780. 5. old.
61	SZÉNÁSSY 1998. 71. old.